由于上个世纪70年代粒子物理标准模型（Standard Model）的提出，量子场论作为理解基本粒子与作用力的理论模型得到了空前的成功，特别是电磁作用力的范畴，例如电子磁矩,实验与理论预测已相互验证到7.6/ 的精密度，然而在强作用力与引力方面，由于理论本身具有的复杂性，相应的理论计算进展相当缓慢。通过简单的数量估计，一个在大型强子对撞机 (LHC) 发生的10胶子散射事件，按照标准的费曼图计算方式需要分析10525900个树图，而在引力子的散射计算方面，由于Einstein-Hilbert引力理论的顶角结构更为复杂，即使单一个4圈层次的散射振幅就是包含 项的亚纯函数，对计算设备是极其严重的挑战。

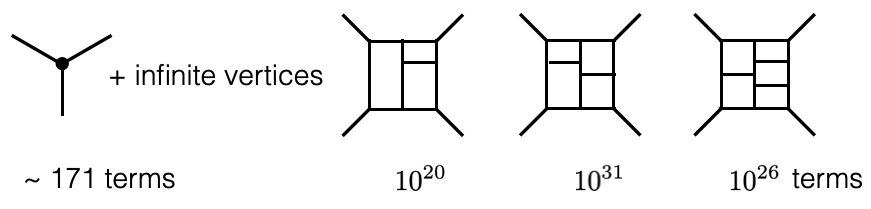
图1. 引力振幅费曼规则计算涉及的项数随圈图修正的精度提高而快速增长

然而另一方面，散射振幅领域在上世纪80年代通过不断的研究积累，发现大量的繁复中间计算结果常最终能化解得到简单的解析表达式，这个重要观察显示现有的量子场论本身具有尚未被完全理解的物理对称性或数学结构，有待更深一层次的研究发掘，散射振幅领域的研究即在通过弦论与各种数学工具来分析规范与引力理论的新对称性并且开发数学上等效于标准费曼规则的振幅建构方式。

基于这个前提，近年来一个重要的新对称性是Bern, Carrasco和 Johansson（BCJ）于2008年所提出的颜色-运动学（colour-kinematics）对偶性。在BCJ的假设中，规范理论振幅可以由数学上等价、形式上更为简单的双伴随（bi-adjoint）标量 理论描述，其中原有结构较为复杂的费曼图可由三顶角图替代，振幅分子中依赖强作用力颜色的部分与依赖动量的部分满足相同的代数关系式，并且规范理论振幅可以表示成结构更为简单、颜色与运动学部分明显对称的形式。BCJ所提出的对偶结构自提出以来，目前已由原本适用的规范理论推广到非线性sigma模型、Dirac-Born-Infeld理论、special-Galilean理论、Einstein-Yang-Mills理论等振幅之中，目前普遍被任务是量子场论中广泛存在的特性之一，并且已成为当前高圈散射振幅计算的最有效理论工具。在这个对偶形式的框架下，BCJ进一步提出了一项对引力振幅研究影响深远的double copy形式，并已使用于LIGO引力波探测的理论分析工作中。

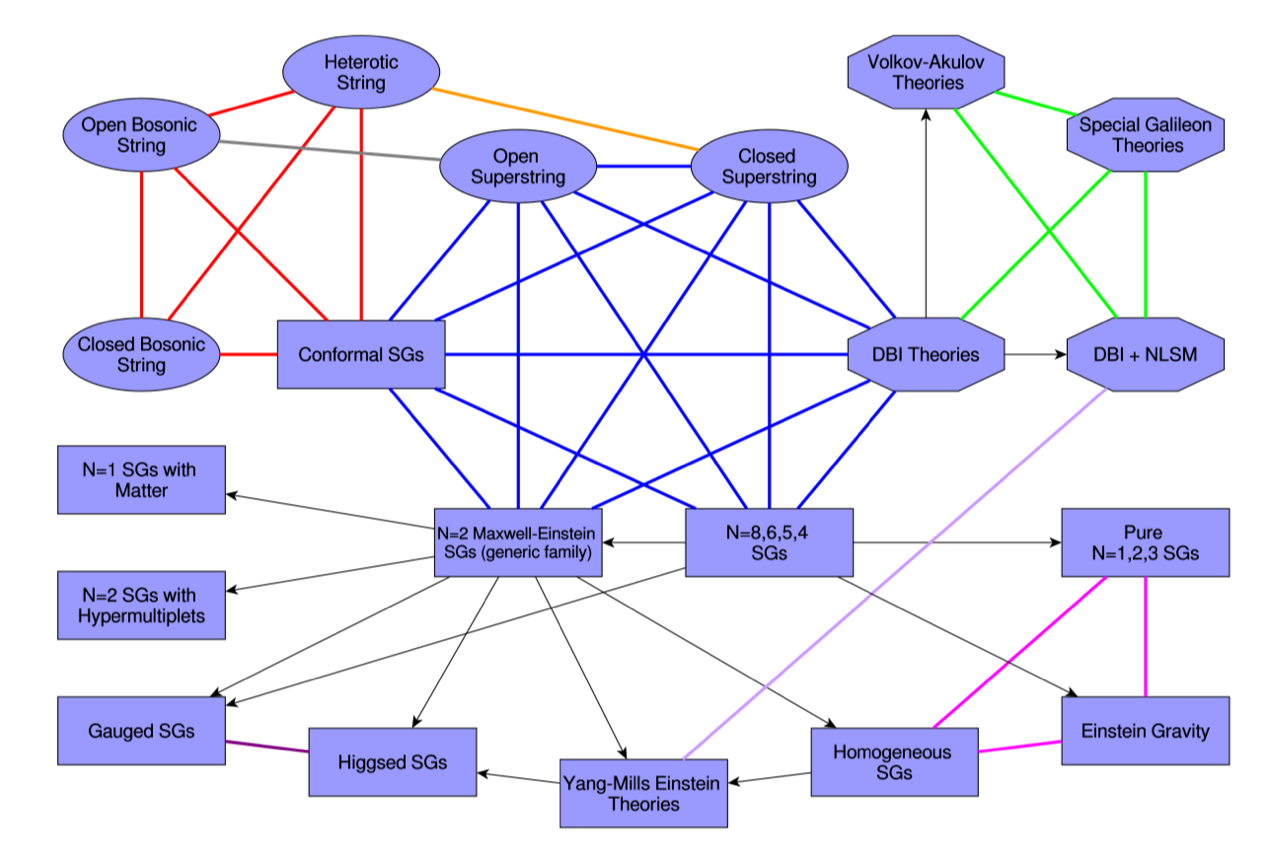
图2. 已知满足颜色-运动学对偶性的物理理论与等效理论（示意图取自arXiv: 1909.01358）

尽管在应用层面上获得了初步的成功，关于BCJ对偶性所预测的运动学代数（kinematic algebra）具体的结构以及其物理成因，自2008年对偶性框架提出以来，一直是散射振幅研究中悬而未解的核心问题之一，部分的原因在于胶子散射振幅本身的结构复杂，分析工作进展相当缓慢。近年来一个重要的突破方式是利用弦论振幅与场论振幅之间的数学联系。尽管弦论作为一个统一四大基本作用力的理论框架目前还有相当多问题有待解决，在散射振幅的研究中弦论常被当作有效的辅助数学工具。一个已知数学上经过严格证明的结果是，弦长趋近于零时，弦论散射振幅在极限下会给出场论散射振幅的结果。

在本篇工作中，傅志豪博士利用开弦振幅的顶点算子代数，成功的把BCJ运动学代数与上世纪苏联时期由列宁格勒学派带领发展的量子群（quantum group）理论关联起来。该工作证明了运动学分子在弦论中的推广自然可以由Dotsenko、Fateev的共形场屏蔽算子建构出，而不同顺序屏蔽算子的作用形成了Drinfeld与Jimbo所提出的q-形变代数结构。在这个图像中，屏蔽算子的对易定义出满足Yang-Baxter方程的R-矩阵。另外该工作指出，由于顶点代数的建构方式帮助我们直接由散射振幅读出运动学代数的根系（root system），这个信息可以使用在弦振幅与Knizhnik-Zamolodchikov（KZ）方程求解问题的对应关系上，从而提高振幅的计算效率。

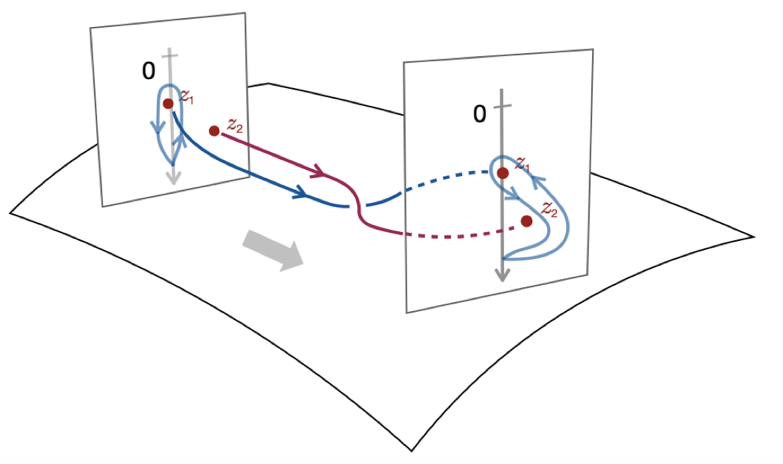
图3. 由Gauss-Manin联络定义出KZ方程解之间的映射关系，从而决定屏蔽算子的R-矩阵

本工作发表于Journal of High Energy Physics (JHEP), 2020年卷，12期，文章号106 DOI: 10.1007/JHEP12(2020)106

受邀于第14届国际李代数与物理应用学术研讨会XIV. International Workshop "Lie Theory and its applications in Physics"大会上做相关工作学术报告